Vamos a poner un ejemplo, un problema que me gustó mucho cuando nos lo contó Francisco Bellot. Pertenece a una de las colecciones de problemas escolares rusos. Este en particular lo podéis encontrar referenciado en Shifman (Ed.): You failed your math test, Comraide Einstein.World Scientific, 2005. Aquí Ian Vardi, nos hace un estudio de los llamados "killer problems" [A. Shen, Entrance Examinations to the Mekh-mat, Mathematical Intelligencer 16 (1994), 6-10], que describen la discriminación que tenían los estudiantes judios en las pruebas de acceso a la facultad de matemáticas en Rusia, entre los años 1970 y 1980. Ian Vardi nos muestra 25 "killer problems" , este hace el número 21 (Smurov, Balsanov, 1986):
Una circunferencia está inscrita en la cara de un cubo de lado a, otra circunferencia circunscrita en la cara contigua. Encuentre la distancia mínima entre los puntos de las circunferencias.
La solución algebraica que nos expone Ian Vardi consiste en parametrizar convenientemente las dos circunferencias en un sistema de coordenadas con origen en el centro del cubo, al calcular la distancia entre dos puntos cualesquiera obtenemos una función en dos variables, basta entonces con calcular el mínimo de esta función.
La gran mayoría de los alumnos que ingresan el primer año en la facultad de matemáticas, es decir, nuestros alumnos de segundo de bachillerato no serían capaces de resolver este problema algebraicamente. Sin embargo desde un punto de vista geométrico, la resolución es mucho más elemental.
Si observamos las dos esferas concéntricas con centro en el centro del cubo y que contienen a cada circunferencia, es evidente que la distancia buscada no puede ser menor que la distancia entre las dos esferas, es decir la diferencia de radios.
Es más, si existiera un radio (de la esfera mayor) que cortara a las dos circunferencias, la mínima distancia sería alcanzada en esos dos puntos.
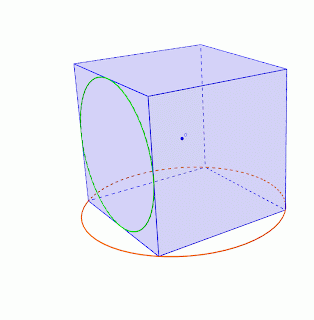
Vamos pues a dibujar esos puntos y demostremos que existen. Consideremos todos los posibles radios que salen del centro y pasan por la circunferencia inscrita ¿Qué tenemos?...Sí, un precioso cono. Ahora cortemos ese cono con el plano que contiene la circunferencia circunscrita. ¿Qué tenemos?...(esto les cuesta más a los alumnos, pero si ya han estudiado las hipérbolas entonces lo ven más fácilmente). Esa rama hiperbólica cortará a la circunferencia circunscrita en dos puntos ( cualquiera nos sirve) dibujemos uno de ellos.
Nota: Si hubiésemos colocado un sistema de referencia con el origen en el centro del cubo, podríamos calcular las ecuaciones algebraicas de todos estos objetos geométricos y ya tendríamos la solución, sin embargo hemos dicho que íbamos a resolverlo de manera geométrica, entonces nada de ecuaciones ;-), aunque sería una forma diferente de llegar a la misma solución que la vista anteriormente, sin utilizar la parametrización ni el cálculo del mínimo en una función de dos variables.
Consideremos los ángulos siguientes: ( el tiedro formado por el radio que hemos dibujado y los radios que unen el centro del cubo con los centros de las dos circunferencias)
Observemos que O1OO2=90º, O1OB=45º, AOO2=α=arctan√2
Cada uno de estos ángulos es menor que la suma de los otros dos, y la suma de los tres es menor que 360º. Estas son condiciones necesarias y suficientes para que exista un triedro de vértice O, cuyos ángulos de las caras sean los tres ángulos marcados. Esto significa que los puntos O, A y B están efectivamente alineados (en la arista común a los dos últimos ángulos del triedro).
Entonces la distancia AB = a (√3-√2) (Diferencia de los radios de las esferas, se calculan fácilmente aplicando Pitágoras a los triángulos rectángulos que forman con los centros de las caras)
Si tomamos otros dos puntos, M y N, en las dos circunferencias, considerando el triángulo OMN, la desigualdad triangular garantiza que la distancia MN es mayor que la diferencia OM-ON, que vale precisamente a (√3-√2), c.q.d.
Las imágenes están tomadas de la versión beta de geogebra 5, en su vista 3D.



No hay comentarios:
Publicar un comentario