Este famoso problema está ligado directamente con el teorema de los números primos, que nos acota la función que nos da el número de primos que hay menor o igual al número dado.
Sabemos que hay infinitos números primos, con lo que podemos encontrar números primos con tantas cifras como queramos, pero no sabemos construir de manera eficiente un algoritmo que factorice un número entero muy grande en sus factores primos, es decir, sin que el tiempo de computo se haga interminable para un ordenador.
Aunque parezca contradictorio, la falta de este algoritmo nos ha dado una solución a la seguridad en las comunicaciones. Uno de los sistemas de cifrado de llave pública más seguros: el RSA, llamado así por sus tres inventores, Ron Rivest, Adi Shamir y Leonard Adleman.
Básicamente consiste en tomar dos primos grandes, p y q, considerar su producto n=p*q y elegir un número e, tal que 1< e < Fi(n) y primo con Fi(n). Esta es la llave pública de cifrado (n, e). La llave privada, la llave de descifrado es (n,d), donde d es el inverso de e módulo Fi(n).
Calcular la llave de descifrado, es decir, calcular d, equivale a calcular Fi(n), lo que es equivalente a su vez a calcular p y q. Si dado cualquier número grande, pudiéramos factorizarlo fácilmente, entonces perderíamos la seguridad del cifrado y todas las comunicaciones que ahora se consideran seguras se verían gravemente afectadas.
¿Fi(n)? ¿inverso de e módulo Fi(n)?...pero de qué me hablas.
Fi(n) es la función de Euler, pero empecemos por el principio:
La criptografía se basa en la utilización de un algoritmo y una clave para codificar un texto de manera que solo pueda ser entendido por aquella persona o entidad que posea la clave para descifrarlo. Partimos de un conjunto finito P , que es nuestro alfabeto. Construimos una aplicación Kc biyectiva:
(texto plano) 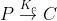 (texto cifrado)
(texto cifrado)
Por ejemplo en Z/2={0,1} solo tenemos dos elementos, los pares y los impares, o cuando hablamos de las 21:00 horas en nuestro reloj las agujas marcan las 9 porque estamos en Z/12.
Esto se llama codificación, la aplicación inversa Kd, es la decodificación. A la función Kc se le llama llave de cifrado y a Kd llave de descifrado. Existen dos tipos de sistemas criptográficos, los sistemas de llave pública (se conoce Kc) y los de llave privada (no se conoce Kc).
Nuestro conjunto finito, puede ser el conjunto de las letras del alfabeto, en nuestro caso 27, aunque podemos ampliarlo con más símbolos que utilizamos al escribir, mayúsculas y minúsculas, signos de puntuación, cifras...Supongamos que trabajamos solo con las 27 letras del alfabeto, a cada letra le asignamos un número entero, entonces nuestro conjunto P={0,1,2,3,4,...26}=Z/27
¿Z/27? ...qué es eso?
Todos conocemos el conjunto de los números enteros Z, que tiene infinitos números, y donde sabemos sumar, restar, multiplicar y dividir. Para poder operar dentro de un conjunto finito, lo que hacemos son clases de números: la clase del cero son el cero y todos los múltiplos de 27, la clase del uno son el uno y todos los números múltiplos de 27 más uno, la clase del dos son el dos y todos los múltiplos de 27 mas dos, y así sucesivamente hasta la clase del 26. En este conjunto, Z módulo 27 o la clase de restos al dividir por 27, están todos los infinitos números de Z.
Dos números pertenecen a la misma clase si su diferencia es un múltiplo de 27, es decir si el resto al dividir por 27 es el mismo, se dice que son congruentes o iguales módulo 27.
Por ejemplo en Z/2={0,1} solo tenemos dos elementos, los pares y los impares, o cuando hablamos de las 21:00 horas en nuestro reloj las agujas marcan las 9 porque estamos en Z/12.
Dentro de estos conjuntos tienen especial interés aquellos que tienen inverso, por ejemplo en Z/6={0,1,2,3,4,5} el 5 tiene inverso que es él mismo ya que 5*5=25=6*4+1=1 mod 6
La función Fi(n), que solemos denotar con la letra griega ) es igual al número de elementos invertibles en Z/n. Veamos un lema importante para el cálculo de estos elementos:
es igual al número de elementos invertibles en Z/n. Veamos un lema importante para el cálculo de estos elementos:
Así si mcd(x,n)=1 entonces existen a y b enteros tales que 1=a*x+b*n, luego a*x=1-b*n con lo que tomando clases en Z/n existe el inverso de x (en este caso es a, puesto que a*x=1 mod n). Recíprocamente si x es invertible en Z/n, existe a tal que a*x=1 + b*n, y 1=a*x-b*n como d=mcd(x,n) es el menor número entero positivo que se puede poner como combinación lineal de x y n, debe ser d=1.
Si n=p primo en Z/p todos los elementos (salvo el cero) son invertibles, luego Fi(p)=p-1. En el caso de una potencia de un primo, n=p^s, los elementos no invertibles son de la forma k*p con 1< k < p^(s-1) luego hay p^(s-1) no invertibles, así Fi(p^s)=p^s-p^(s-1)=(p-1)p^(s-1). Y en general se tiene:
Dado x en Z/n, x es invertible si y solo si mcd(x,n)=1.
Luego los elementos que tienen inverso son los coprimos con n (x y n son primos entre si, no tienen factores primos comunes). La demostración de este lema se basa en la propiedad del máximo común divisor (llamada Identidad de Bezout) que nos asegura que si d=mcd(x,n) entonces existen números a y b de Z tales que d=a*x+b*n siendo d el menor número entero positivo que se puede poner en combinación lineal de x y n.Así si mcd(x,n)=1 entonces existen a y b enteros tales que 1=a*x+b*n, luego a*x=1-b*n con lo que tomando clases en Z/n existe el inverso de x (en este caso es a, puesto que a*x=1 mod n). Recíprocamente si x es invertible en Z/n, existe a tal que a*x=1 + b*n, y 1=a*x-b*n como d=mcd(x,n) es el menor número entero positivo que se puede poner como combinación lineal de x y n, debe ser d=1.
Si n=p primo en Z/p todos los elementos (salvo el cero) son invertibles, luego Fi(p)=p-1. En el caso de una potencia de un primo, n=p^s, los elementos no invertibles son de la forma k*p con 1< k < p^(s-1) luego hay p^(s-1) no invertibles, así Fi(p^s)=p^s-p^(s-1)=(p-1)p^(s-1). Y en general se tiene:
Por ejemplo, en el caso Z/6, 6=2*3, el número de invertibles es Fi(6)=(2-1)*(3-1)=2, que son la clase del 1 y la clase del 5 como hemos visto.
Una propiedad importante para el cálculo de potencias grandes en Z/n es la siguiente:
Para demostrar esta propiedad se consideran todos los elementos invertibles de Z/n, se multiplican cada uno de ellos por a, que al ser primo con n resultan ser todos diferentes, luego son todos los elementos invertibles de Z/n.
%7D%5C%7D=%5C%7Bar_1,%5Ccdot&space;%5Ccdot&space;%5Ccdot&space;ar_%7B%5Cvarphi&space;(n)%7D%5C%7D)
Y como son invertibles podemos dividir por el producto de los ri, demostrando así la propiedad.
Con todo esto ya podemos volver al RSA y ver que efectivamente las dos funciones son inversas:
La función de cifrado, con e primo con Fi(n), luego e tiene inverso en Z/Fi(n).
=p%5E%7Be%7D%5C,&space;mod%5C,n&space;%5Cend%7Bmatrix%7D)
=c%5E%7Bd%7D%5C,&space;mod%5C,n&space;%5Cend%7Bmatrix%7D)
)=f(c%5Ed)%3Dc%5E%7Bed%7D%3Dc%5E%7B1+%5Clambda&space;%5Ccdot&space;%5Cvarphi&space;(n)%7D=c%5Ccdot&space;(c%5E%7B%5Cvarphi&space;(n)%7D)%5E%5Clambda&space;=c%5Ccdot&space;1%5C,&space;mod%5C:&space;n=c%5C;&space;mod%5C:&space;n)
En la práctica, si N es nuestro alfabeto, los mensajes van a ser bloques de k-letras (texto plano) y los mensajes cifrados serán bloques de l-letras:
Tomando k < l enteros positivos de modo que los bloques sean de aproximadamente 200 cifras, y fijando n=p*q comprendido entre N^k y N^l. Utilizando la aplicación biyectiva siguiente:
Veamos un ejemplo, no es práctico porque no vamos a tomar números grandes para facilitar los cálculos, pero puede sacarnos de dudas. Supongamos que queremos cifrar la palabra HOLA, esta se corresponde con (8,16,12,1). Si tomamos grupos de cuatro letras, debemos buscar n=p*q entre 27^4= 531441 y 27^5=14348907. Tomamos por ejemplo los primos p=1201 y q=2551, n=p*q=3063751.
Buscamos nuestra clave pública, calculamos Fi(n)=Fi(3063751)=Fi(1201)*Fi(2551)= 1200*2550= 3060000 =2^5 * 3^2 * 5^4*17 , tomamos por ejemplo e=7 que es primo con Fi(n). Esta será nuestra llave pública Kc(n=3063751, e=7)
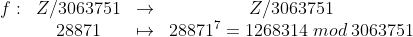
&space;%5Cend%7Bmatrix%7D)
Y finalmente obtenemos el texto cifrado (16,21,11,10,2) se corresponde con OTHJB.
Nota: la letra Z coincide con el número 27 que es la clase del cero. A ver si sacáis el mensaje!
Este post forma parte del Carnaval de Matemáticas, que en esta septuagésima novena edición, también denominada 9.3, está organizado por @juanfisicahr a través de su blog Esto no entra en el examen.
Una propiedad importante para el cálculo de potencias grandes en Z/n es la siguiente:
Para demostrar esta propiedad se consideran todos los elementos invertibles de Z/n, se multiplican cada uno de ellos por a, que al ser primo con n resultan ser todos diferentes, luego son todos los elementos invertibles de Z/n.
Tomando su producto también será igual:
Y como son invertibles podemos dividir por el producto de los ri, demostrando así la propiedad.
Con todo esto ya podemos volver al RSA y ver que efectivamente las dos funciones son inversas:
La función de cifrado, con e primo con Fi(n), luego e tiene inverso en Z/Fi(n).
La función de descifrado, con d el inverso de e mod Fi(n):
Comprobamos que son inversas:
En la práctica, si N es nuestro alfabeto, los mensajes van a ser bloques de k-letras (texto plano) y los mensajes cifrados serán bloques de l-letras:
Tomando k < l enteros positivos de modo que los bloques sean de aproximadamente 200 cifras, y fijando n=p*q comprendido entre N^k y N^l. Utilizando la aplicación biyectiva siguiente:
Veamos un ejemplo, no es práctico porque no vamos a tomar números grandes para facilitar los cálculos, pero puede sacarnos de dudas. Supongamos que queremos cifrar la palabra HOLA, esta se corresponde con (8,16,12,1). Si tomamos grupos de cuatro letras, debemos buscar n=p*q entre 27^4= 531441 y 27^5=14348907. Tomamos por ejemplo los primos p=1201 y q=2551, n=p*q=3063751.
Buscamos nuestra clave pública, calculamos Fi(n)=Fi(3063751)=Fi(1201)*Fi(2551)= 1200*2550= 3060000 =2^5 * 3^2 * 5^4*17 , tomamos por ejemplo e=7 que es primo con Fi(n). Esta será nuestra llave pública Kc(n=3063751, e=7)
Y finalmente obtenemos el texto cifrado (16,21,11,10,2) se corresponde con OTHJB.
Veamos la función inversa para descodificar el mensaje cifrado, para ello necesitamos el inverso de e=7 módulo 3060000. Podemos utilizar el Algoritmo extendido de Euclides , que en este caso es sencillo pues solo tenemos que hacer dos divisiones:
3060000=7*437142+6
7=6*1+1
luego 1=7*437143-3060000, y la clase inversa del 7 es 437143 mod 3060000. Esta es nuestra llave privada Kd(n=3063751, d=437143):
Pasamos al conjunto Z/27^4 escribiendo el número en base 27: 28871=8+16*27+12*27^2+1*27^3 obtenemos las correspondientes letras (8,16,12,1)=HOLA.
Os propongo que con mi clave pública (n=3063751, e=7) me escribáis algún mensaje codificado en los comentarios. Para los cálculos os propongo utilizar la versión online de Sage. Aquí os dejo una introducción que os puede ayudar.
Y aquí mi mensaje cifrado que podéis descifrar con la clave privada Kd(n=3063751, d=437143)
Os propongo que con mi clave pública (n=3063751, e=7) me escribáis algún mensaje codificado en los comentarios. Para los cálculos os propongo utilizar la versión online de Sage. Aquí os dejo una introducción que os puede ayudar.
Y aquí mi mensaje cifrado que podéis descifrar con la clave privada Kd(n=3063751, d=437143)
UZJTZ-ÑOIBE-DTPRC
Este post forma parte del Carnaval de Matemáticas, que en esta septuagésima novena edición, también denominada 9.3, está organizado por @juanfisicahr a través de su blog Esto no entra en el examen.

No hay comentarios:
Publicar un comentario